Lernspiel: Wie weit sind die Sterne eigentlich entfernt?
Diese Frage hat sich jeder Mensch in seinem Leben mehr als einmal gestellt. Besonders unter Kindern ist sie sehr beliebt.
Die App ermöglicht den Schülerinnen und Schülern (und allen Interessierten) einen spielerischen Zugang zur Entfernungsmessung der Sterne. Das Lernspiel greift dabei auf den Effekt der Parallaxe zurück. Die App bietet einen runden Rahmen, in welchem den Spielerinnen und Spielern die Methode erklärt und anschließend die Entfernung eines noch unbekannten Sterns erforscht wird. Durch die Lerneinheit führt eine Mutter mit ihrer Tochter, sodass ein zusammenhängender Bogen gespannt wird.
Zielgruppe
Das Lernspiel richtet sich primär an die Schülerinnen und Schüler der Sekundarstufe I in der siebten bis neunten (bzw. zehnten) Jahrgansstufe. Die verfügbaren Versionen umfassen eine Android und Windows (32bit und 64bit) Version. Die Android Version wird (zukünftig) im Google Play Store zum Download angeboten. Das Lernspiel wurde bereits auf verschiedensten Geräten hinsichtlich der Funktionalität getestet.
Aufbau und Durchführung
Zur Einführung wird eine kurze Animation gezeigt, welche die Problemstellung der Entfernungsmessung einführt. Die Lerneinheit ist an die Struktur des problemorientierten Unterrichts angegliedert. Anschließend folgt eine kurze Tour durch unser Universum. Dadurch erhalten die Spielerinnen und Spieler einen allgemeinen Überblick über unser Sonnensystem und die Entfernung der Sterne.
Als nächste Station wird der Effekt der Parallaxe bei einer Autofahrt erforscht und in einem kurzen Merksatz festgehalten. Daran anschließend wird die Entfernungsberechnung den Spielenden erklärt und selbstständig erprobt. Zuletzt wird das erworbene Wissen auf die Sterne übertragen. Die Schülerinnen und Schüler beobachten die Sterne und können die Parallaxe entdecken und simulieren. Es ergibt sich eine Verbindung zwischen der Parallaxe und der Entfernung eines Sterns. Nun wird die Entfernung eines noch unentdeckten Sterns bestimmt. Zum Abschluss können die Schülerinnen und Schüler in einem kurzen Quiz ihr Wissen unter Beweis stellen.
Besonderheiten des Lernspiels
Das Spiel umfasst drei Schwierigkeitsgrade und ist in der deutschen und englischen Sprache verfügbar. Der Schwierigkeitsgrad und die Sprache können zu jedem Zeitpunkt gewechselt werden. Alle Dialoge und Animationen sind in beiden Sprachen vertont. Die Lautstärke kann individuell angepasst werden. Es gibt in den kniffeligen Abschnitten Hilfen, die bei Bedarf aktiviert werden können. Sie umfassen kleine Animationen, benötigte Formeln und einen kleinen Taschenrechner.
Zusätzlich ist das Spiel mit einen „Shortcut“-System ausgestattet. Dadurch kann das Lernspiel unterbrochen/ pausiert und später fortgesetzt werden.
Material
Zusätzlich gibt es neben dem Lernspiel ein begleitendes Arbeitsblatt für Schülerinnen und Schüler, sowie einem kurzen informativen Text für Lehrkräfte. In diesem werden die wichtigsten physikalischen Aspekte zur Entfernungsmessung in aller Kürze ausgeführt.
Information zur Entfernungsbestimmung von Sternen
Parallaxe:
Die Basis der Entfernungsbestimmung eines Sterns, wie sie in diesem Lernspiel durchgeführt wird, ist die Parallaxe. Als Parallaxe wird die scheinbare Bewegung eines beobachteten Objektes beschrieben, wenn der/die Beobachtende die Position verändert. Ein klassisches Beispiel ist das Ablesen einer analogen Anzeige. Der richtige Wert wird durch senkrechtes Ablesen erreicht. Ein schräger Blick auf die Anzeige „verschiebt“ den Zeiger.
Parallaxe in der Astronomie:
Bei der Beobachtung der Sterne tritt der Effekt der Parallaxe ebenfalls auf, da wir als Beobachter auf der Erde unsere Position, relativ zu den Sternen, verändern. Durch die Rotation der Erde um die Sonne sehen wir den Stern unter verschiedenen Perspektiven. Wie die Abbildung 1 zeigt, sehen wir einen näheren Stern vor dem (unendlich) weit entfernten Hintergrund von Sternen in einer elliptischen Bahn kreisen. Die Form der Ellipse wird durch die Lage des Sterns relativ zur Erdbahn-Ebene bestimmt. Steht der Stern wie in der Abb. 1 im 90° Winkel zur Erdbahn, sehen wir eine Kreisbewegung. Je flacher der Winkel ausfällt, desto gestauchter wird der Kreis, wir sehen eine Ellipse. Der gemessene Parallaxenwinkel π ergibt sich aus zwei festen Messpunkten. Nähere Objekte haben eine größere elliptische Bewegung und dadurch einen größeren Parallaxenwinkel, als jene weiter entfernte.

Entfernungsbestimmung:Determining the distance:
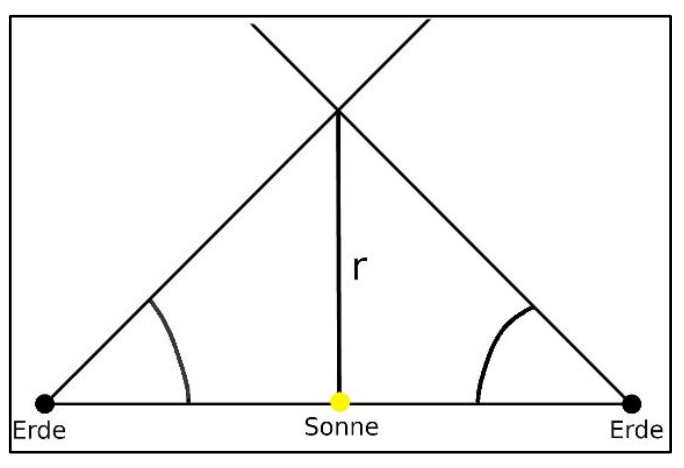
Mithilfe des Winkels π kann die Entfernung des Sterns berechnet werden. Dazu kann mithilfe der trigonometrischen Funktionen folgende Beziehung aufgestellt werden (siehe Abb. 2).
Letztere Approximation folgt aus der Kleinwinkelnäherung des Tangens. Dies ist zulässig, da die Winkel der Parallaxe π sehr klein sind. Im Lernspiel wird die Entfernungsberechnung nicht über den Winkel π direkt, sondern indirekt über den Winkel des Teleskops auf der Erde (in Abb. 2 der Winkel unten rechts) durchgeführt. Dies ermöglicht die gleichzeitige Bestimmung des Abstands durch die Konstruktion eines Dreiecks und die Berechnung mithilfe des Tangens. Dazu wird die Grundlinie vorgegeben. Die gemessenen Winkel des Teleskops werden eingetragen und das Dreieck konstruiert. Mithilfe des Maßstabs wird die Entfernung berechnet.


Downloads
- Einführungsvideo Deutsch (.mp4)
- Einführungsvideo Deutsch Englisch (.mp4)
- Android (.apk)
- Windows 64bit (.zip)
- Windows 32bit (.zip)
- iOS Apple (noch nicht getestet) (.zip)
- Arbeitsblatt für Schülerinnen und Schüler (.pdf)
- Informationsblatt für Lehrkräfte (.pdf)
Alle angebotenen Inhalte von Jan-Niklas Hissel.
Making of
Entwicklung des Lernspiels
Das Lernspiel entstand im Rahmen meiner Masterarbeit an der Universität zu Köln. Das Spiel wurde mit Unity programmiert und die 3D Modelle, sowie die Animationen, wurden in Cinema 4D erstellt.
Die Mutter wird in der deutschen und englischen Version von Lucia Gatzweiler und die Tochter von Kim Nguyen gesprochen.
Educational game: How far away are the stars?
Information on determining the distance of stars
Parallax:
The underlying concept for the determination of the distance of a star, as it is shown in the educational game, is the parallax. The parallax is the apparent movement of an object along two different lines of sight. A typical example is the reading of a scale. A different point of view „changes“ the position of the indicator.
Parallax in astronomy:
While observing the stars we will encounter the parallax, because the observer on Earth changes his position relative to the star. During the orbit of the Earth around the sun, we will observe the star from different angles. As shown in Figure 1, the observed star appears to move in an elliptic path in front of a background, that is fixed and (endlessly) far away. The shape of the ellipsis depends on the position of the star relative to Earth’s orbit. If the star is at an angle of 90° to the plane of Earth’s orbit (Figure 1), we will observe a perfect circular movement of the star. The smaller the angle gets, the more flattended the circular movement becomes and we can see an ellipse. The parallaxe angle 𝜋 can be measured between two fixed points. Closer objects have a larger ellipse an therefore a greater parallax angle.

Determining the distance:
By using the parallax angle 𝜋, one can calculate the distance of the star. The trigonomic functions connect the distance 𝑟 to the angle 𝜋 according to Figure 2.
The last approximation is a result of the small-angle approximation of the tangent. The approximation is valid, because the parallax angles are very small. Within the game, the distance is not determined with the angle 𝜋. Instead, the angle of the telescope on earth is used (the angle on the bottom right of Figure 2). This allows the construction of a triangle which makes the calculation of the distance 𝑟 with the tangent and a geometric contruction of 𝑟 possible. For that the baseline of the triangle is given by the distance of Earth and sun. The angles of the telescope are measured and drawn on the baseline. The triangle can now be constructed and with the use of a proper scale, the students can convert the measured length of 𝑟 to the real distance of the star.



Downloads
- Introduction video Englisch (.mp4)
- Android (.apk)
- Windows 64bit (.zip)
- Windows 32bit (.zip)
- iOS Apple (not yet tested) (.zip)
- Information sheet for teachers (.pdf)
All content offered by Jan-Niklas Hissel.